Message Passing Programming

MPI modes

Different Send

SsendBsendSend

Full form

Synchronous Send

Buffered Send

standard Send

Synchronous?

Guaranteed to be synchronous

Guaranteed to be asynchronous

may be both

Behavior

Routine will not return until message has been delivered.

Routine immediately returns.

Bsend when buffer is not full, Ssend when buffer is full.

Impact

May result in forever waiting.

System helps copy data into a buffer and sends it later on.

Unlikely to fail.

To elaborate:

  • Ssend will wait until the receiver calls Recv, therefore it will waste the waiting time and even result in forever waiting (deadlock) if the receiver does not call.

    • Can be used to debug the deadlock situation by replacing Send with Ssend.

  • Bsend will copy values into system buffer, and returns immediately, the sending data can be overwritten after that. When the receiver calls Recv, system will send the data in the buffer to the receiver.

    • If Recv is called earlier than the Bsend, since Recv is always synchronous, the receiver will be blocked in this function until Bsend is issued.

    • User should provide enought buffer space in Bsend by using MPI_Buffer_attach.

    • If there is not enough space, Bsend will FAIL.

    • Not encouraged to use, because when it is not feasible to correctly compute the amount of buffer that is needed, it will cause unrecoverable error. Ref

    • Also Noted: BSend is different from non-blocking Send (i.e. Isend).

  • MPI_Send tries to solve problems above by:

    • Allocate buffer space by system.

    • Behave Asynchronous when buffer has space, behave Synchronous when buffer is full.

    • Corner case of MPI_Send:

    Process A and Process B both run Send() & Recv() to the other, will deadlock if anyone's Send becomes synchronous. Correct way to avoid deadlock: either match sends and receives explicitly instead of determining by system. e.g. ping-pong send&recv.

MPI_Probe

  • For checking whether the messages have arrived, use MPI_Probe. The usage is the same as MPI_Recv except no receive buffer specified.

  • int MPI_Probe(int source, int tag, MPI_Comm comm, MPI_Status * status) in MPICH.

  • Status is set as if the receive took place, it contains count, cancelled, MPI_SOURCE, MPI_TAG, MPI_ERROR.

  • Be careful when using wildcards like MPI_ANY_SOURCE to probe message, SHOULD specify the source rank when receiving messages by MPI_Recv(buffer, count, datatype, probe_status.MPI_SOURCE, ...)

  • Noted: In OpenMPI 4.1.1 version, the count and cancelled values are used inside, users are not supposed to fetch it, it will not return what users actually want.

// In OpenMPI: ompi/include/mpi.h.in
/*
 * MPI_Status
 */
struct ompi_status_public_t {
    /* These fields are publicly defined in the MPI specification.
       User applications may freely read from these fields. */
    int MPI_SOURCE;
    int MPI_TAG;
    int MPI_ERROR;
    /* The following two fields are internal to the Open MPI
       implementation and should not be accessed by MPI applications.
       They are subject to change at any time.  These are not the
       droids you're looking for. */
    int _cancelled;
    size_t _ucount;
};
typedef struct ompi_status_public_t ompi_status_public_t;

Tag

  • Every message can have a Tag

    • non-negative integer value

    • maximum value can be queried using MPI_TAG_UB attribute

    • MPI guarantees to support tags of at least 32767

    • Most programs set tag to zero for convenience.

  • Can be useful for filtering messages, choosing to receive messages with specific tag. Also in Debugging, always tag messages with the rank of the sender.

  • Most commonly use the wildcards MPI_ANY_TAG, which means accept all messages regardless of the tag, and later finds out the actual tag value by looking at the MPI_Status.

Communicator

  • All MPI communications take place within a communicator.

    • a communicator is a group of processes.

    • Commonly use the pre-defined communicator: MPI_COMM_WORLD which involves ALL processes.

    • MPI_COMM_SELF contains only one self process in contrast.

  • Communicator has no wildcards, messages can only be transferred in one comm.

  • int MPI_Comm_split(MPI_Comm comm, int color, int key, MPI_Comm *newcomm) in MPICH

    • color decides the sub-communicator, key decides the new rank in new comm.

    • Algorithm:

    • Use MPI_Allgather to get the color and key from each process

    • Count the number of processes with the same color; create a communicator with that many processes. If this process has MPI_UNDEFINED as the color, create a process with a single member.

    • Use key to order the ranks

  • int MPI_Comm_dup(MPI_Comm comm, MPI_Comm * newcomm) in MPICH can duplicate an existing communicator with all its cached information (not limited to MPI_COMM_WORLD).

  • Enables processes to communicate with each other safely within a piece of code

    • Essential for people writing parallel libraries (e.g. FFT) to avoid library messages becoming mixed up with user messages.

    • Isolation guaranteed by communicator is stronger than Tag value because of the wildcard of latter one.

  • Bad practice to use MPI_COMM_WORLD explicitly in the routines, better using a variable which allows for greater flexibility later on. e.g.

MPI_Comm comm;
comm = MPI_COMM_WORLD;
int rank, size;
MPI_Comm_rank(comm, &rank);
MPI_Comm_size(comm, &size);

Traffic Flow

Definition:

  • divide road into a series of cells

    • either occupied or unoccupied

  • perform a number of steps

    • each step, cars move forward if space ahead is empty

  • Circle road: if a car moves off the right, it appears on the left.

    • i.e. identity cell N+1 with cell 1, and cell 0 with cell N

Cell Update Rule:

  • If old(i) = 0, it means cell i is empty, the next status is decided by whether cell i-1 has car.

i-1\i+101

0

0

0

1

1

1

  • If old(i) = 1, it means cell i is not empty, the next status is decided by whether it can move forward to cell i+1 if cell i+1 is empty.

i-1\i+101

0

0

1

1

0

1

To conclude, it can be represented as below in mathematics: $new_i = (old_i&old_{i+1}) | ((!old_i)&old_{i-1})$

Solve

  1. Split the data into nprocs, initialize at rank 0 and send to other ranks.

  2. In every iteration:

    1. Recv old[0] from last rank old[n]

    2. Recv old[n+1] from next rank old[1]

    3. Send old[1] to last rank old[n+1]

    4. Send old[n] to next rank old[0]

    5. Swap the Send and Recv order according to the odd-even of rank to avoid deadlock.

  3. Sum reduce the move count of each rank to master rank.

Result:

nprocsMCOPs+OPENMP

serial-1

113.23

955.58

2

140.44

142.75

4

276.09

1811.29

8

530.58

1856.21

16

1012.64

1842.6

32

1496.01

1495.96

48

2008.33

1939.41

Interesting Found:

  1. Only apply OpenMP can achieve satisfying result as well, from 113 to 955.58.

  2. MPI+OpenMP does not perform well when nprocs is 2 and 32.

  3. Apart from nprocs is 2 and 32, other MPI+OpenMP combinations can reach similar performance.

  4. Is ./traffic the same as mpirun -n 1 traffic (the same binary file) ?

    • ./traffic is much faster than mpirun -n 1 traffic, MCOPs 989.14 compared to 110.28, maybe because getting rid of MPI_Env setup?

Message-Passing Strategy

  1. Broadcast data to 2 processes

  2. Split calculation between 2 processes

  3. Globally resynchronize all data after each move

Analogy: In deep learning, it is similar to data parallelism. In data parallelism, each worker holds an entire copy of model and trains different data. After each epoch, all workers share the weight learned from its part of data.

Parallelisation Strategy

  1. Scatter data between 2 processes: distributed data strategy

  2. Internal cells can be updated independently.

  3. Must communicate with neighboring processes to update the edge cells.

  4. Sum local number of moves on each process to obtain total number of moves at each iteration.

Analogy: In deep learning, it is similar to model parallelism. In model parallelism, each worker has a part of model and need to pass the boundary value to the next partial model to pipeline the whole training.

Non-Blocking Communications

Difference:

synchronous / asynchronous is to describe the relation between two modules. blocking / non-blocking is to describe the situation of one module. Reference here

Synchronous mode affects completion, while blocking-mode affects initialization.

  • Non-blocking calls return straight away and allow the sub-program to continue to perform other work. At some later time the sub-program can test or wait for the completion of the non-blocking operation.

  • All non-blocking operations should have matching wait operations. Some systems cannot free resources until wait has been called.

  • A non-blocking operation immediately followed by a matching wait is equivalent to a blocking operation.

  • Non-blocking operations are not the same as sequential subroutine calls as the operation continues after the call has returned (in background).

Separate communication into three phases:

  1. Initiate non-blocking communication.

  2. Do some other works.

  3. Wait for the non-blocking communication to complete.

Send

Related functions matrix (Link to MPICH):

SynchronousBuffered

Blocking

MPI_Ssend

MPI_BSend

Non-blocking

MPI_Issend

MPI_Ibsend

Receive

int MPI_Irecv(void *buf, int count, MPI_Datatype datatype, int source, int tag, MPI_Comm comm, MPI_Request *request) in MPICH

  • Send and receive can be blocking or non-blocking.

  • A blocking send can be used with a non-blocking receive, and vice-versa.

Test & Wait

MPI_Ixxx will return a request handle, which can be used for future detect, by Test or Wait.

Related functions matrix (Link to MPICH):

TestWait

Specified One

MPI_Test

MPI_Wait

Anyone

MPI_Testany

MPI_Waitany

Some

MPI_Testsome

MPI_Waitsome

All

MPI_Testall

MPI_Waitall

SendRecv combination

int MPI_Sendrecv(const void *sendbuf, int sendcount, MPI_Datatype sendtype, int dest, int sendtag, void *recvbuf, int recvcount, MPI_Datatype recvtype, int source, int recvtag, MPI_Comm comm, MPI_Status *status) in MPICH

  • Specify all send/receive arguments in one call

    • MPI implementation avoids deadlock

    • useful in simple pairwise communication patterns, but not as generally applicable as non-blocking.

Possible implementations:

  1. determine the send and recv sequence by the rank, e.g. ping

    if (rank == 0) {
  MPI_Send(...);
  MPI_Recv(...);
} else if (rank == 1) {
  MPI_Recv(...);
  MPI_Send(...);
}

  2. Use Non-blocking mode and Wait later. e.g.

    MPI_Isend(..., send_handler, ...);
MPI_Irecv(..., recv_handler, ...);
MPI_Wait(send_handler);
MPI_Wait(recv_handler);

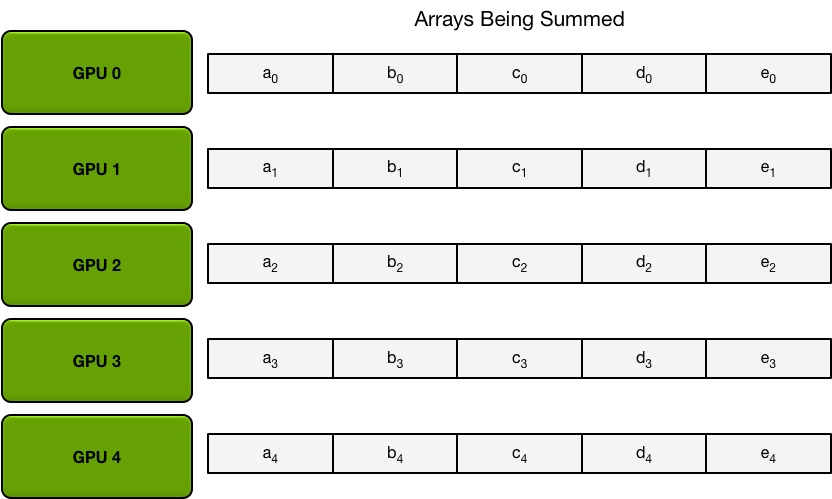
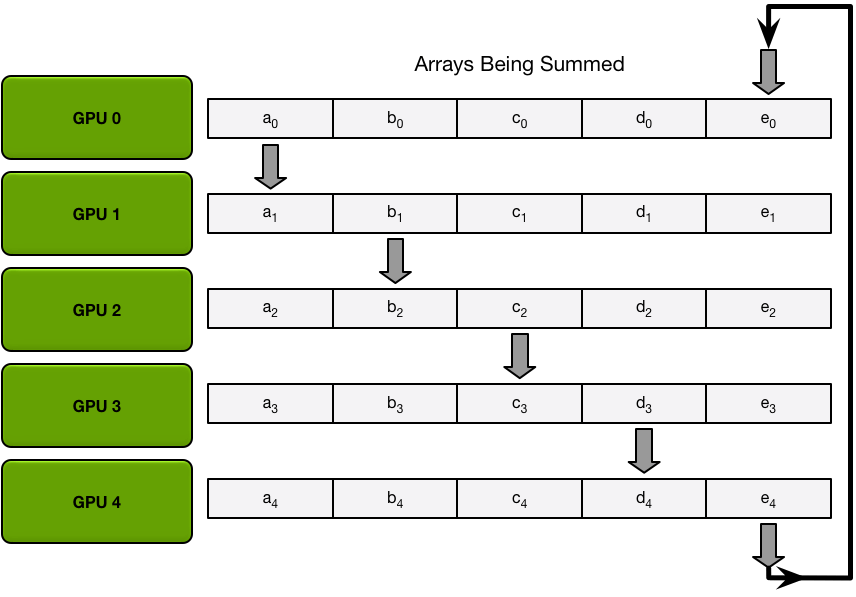
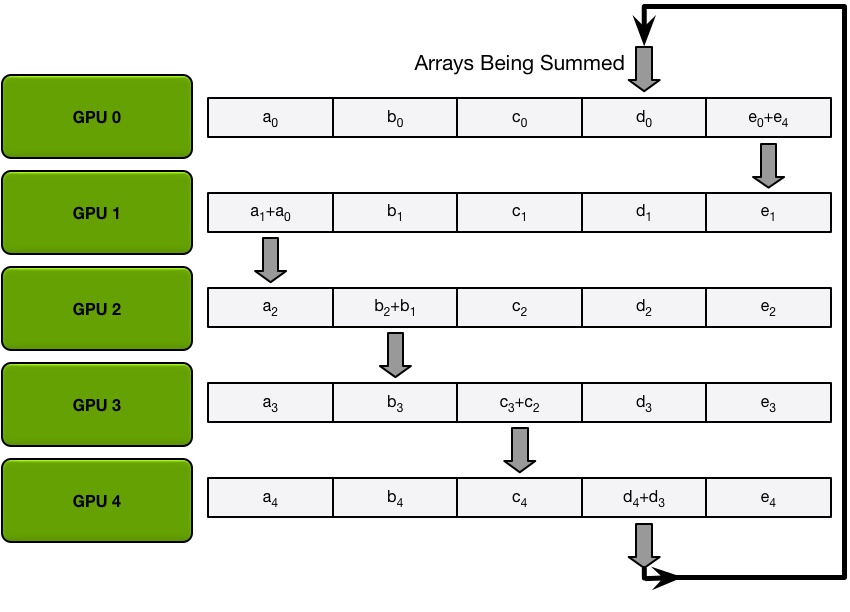
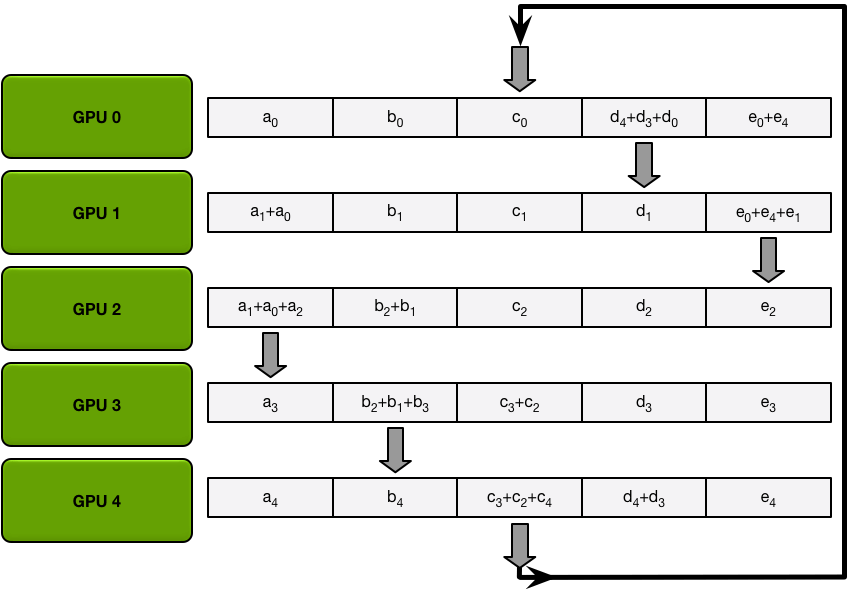
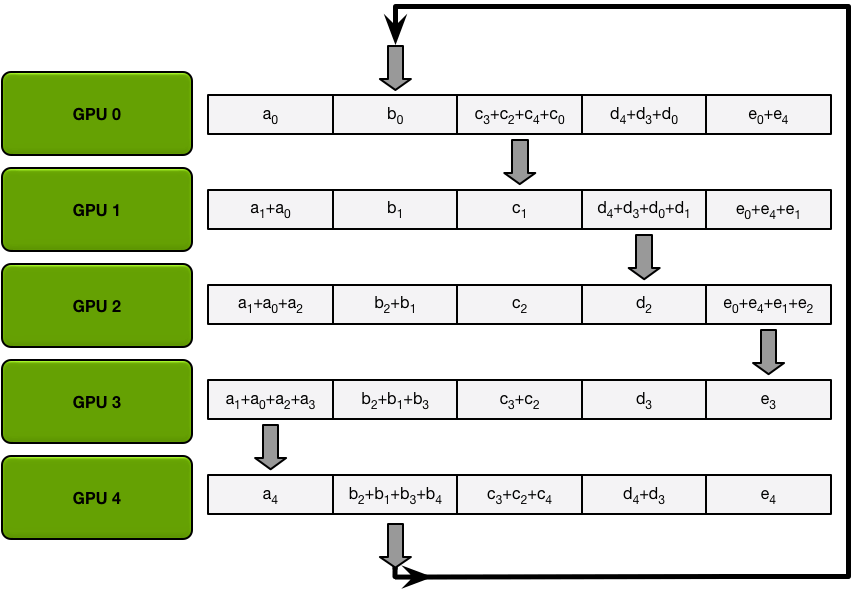
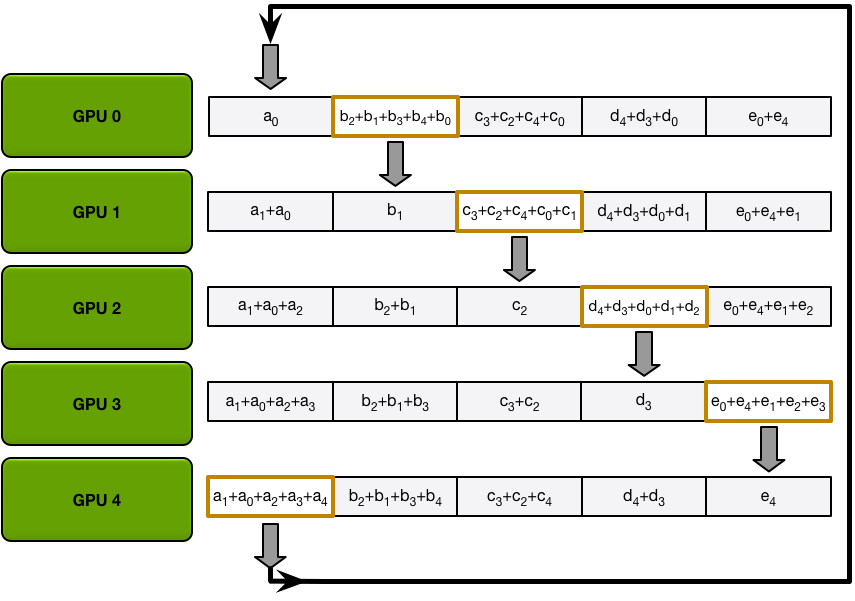
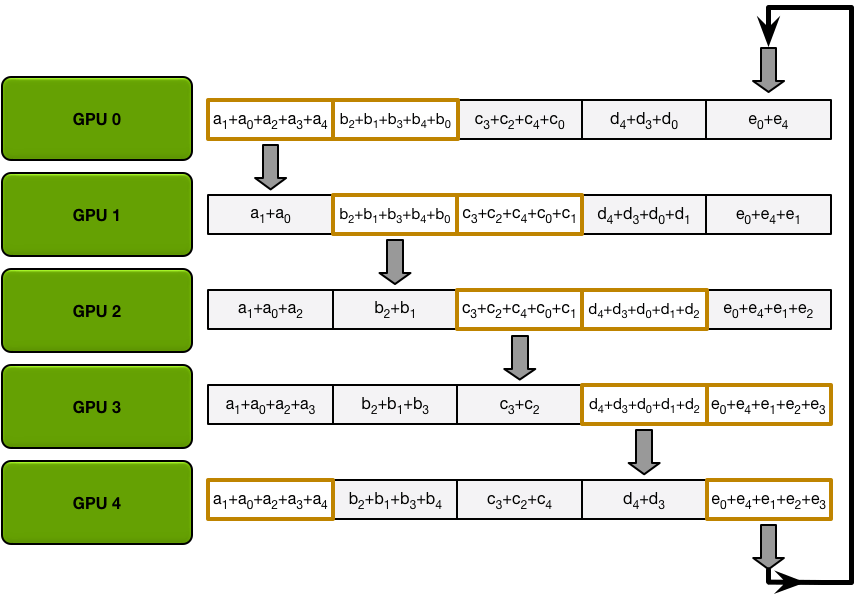
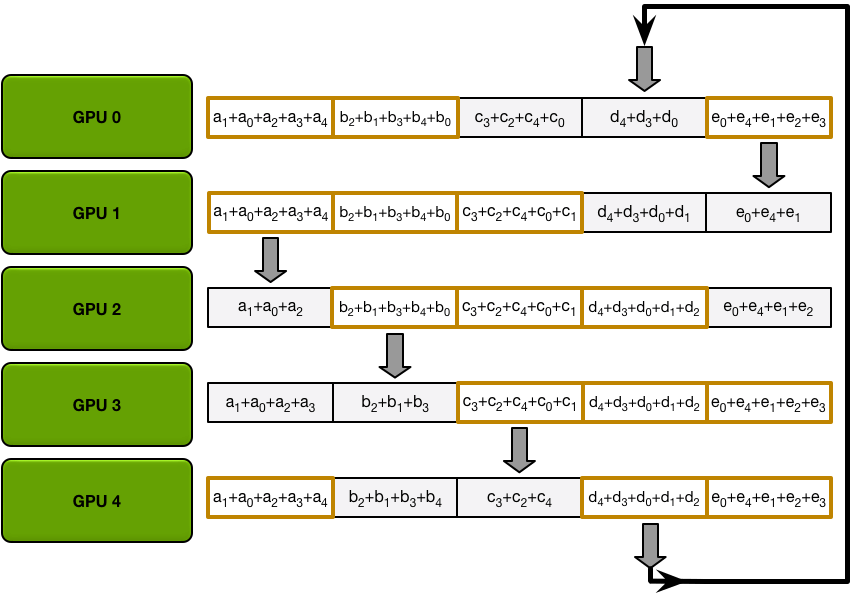
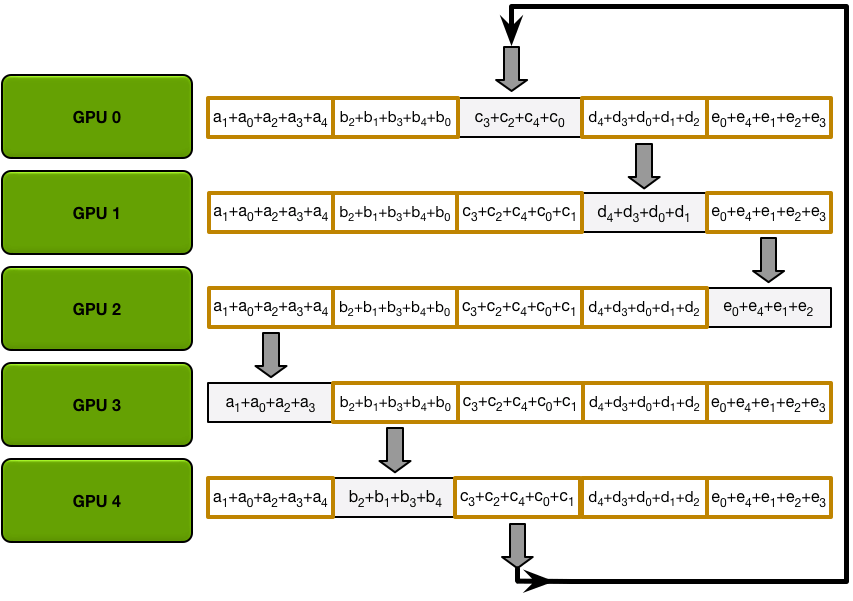
Send and recv as a ring situation: In deep learning, the AllReduce reduction can be achieved by Ring AllReduce, each worker receives a partial from the backward neighbor and sends a different partial to the forward neighbor. After N times, all workers have accumulated a fixed partial from all other workers, and then broadcast its completed part to others. Details can be seen on this blog.

PreviousMPI OverviewNextOpenMP Overview

Last updated